Use the menu on the right to choose the section you are interested in.
The soroban
The soroban is the japanese abacus, that evolved from the chinese abacus (the suanpan) by removing one heaven bead and one earth bead, to only keep the bare minimum to interact with numbers.
What distinguishes it from the suanpan, is not only its number of beads, but also the shape of the beads. They are biconal, (made of 2 cones), with a thin slice that made it easier to manipulate bead and move them up and down.
The parts
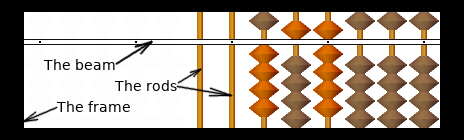
- The frame
- The frame is the black outline that holds together the soroban parts.
- The beam
- The beam (also called the reckoning bar) is the bar that splits the soroban in 2 horizontally.
- The rods
- The rods or columns are the stem that holds the beads. Their number defines the size of the soroban. Most of the time, it is 21, but that can vary from 13 to 31 or even more. The bigger the soroban is, the more numbers or the bigger the numbers you can put on it.
- The beads
- The beads are the basic part of the soroban that are able to be moved on the rods. You can move them up or down, given they current position.
How to read a number on the soroban
1. Let's learn with an example
What is the number displayed on the little soroban below ?

2. Rods
First, we notice there are 4 vertical rods with beads at different positions. So the number has 4 digits.

4. First rod and earth beads
5. Heaven bead
6. Second rod
7. Third rod
8. Fourth rod
How to add 2 numbers
To add numbers on the soroban, you proceed in a very similar way that you do addition on paper. You go on, digit by digit, column by column, with any carry that you might need. One notable difference is that you proceed from left to right.
To sum it up, you basically have to put on the soroban the number you want to add. In the most simple case, you add the beads for each digit on each rod. In others, you have to do a little gymnastic that becomes an automatism other time.
Adding one digit at a time


13 + 21 — Let's see this on an example: say we have 13 on the soroban; and wanted to add 21.
So first, let's add 2 on the dozen rod. Let's activate 2 beads. Then on the unit rod, let's add 1 by activating one bead. We finally, get 34.
So we see that to add a digit on a row, we simply activate the needed beads that we want to add.
The same principle holds true for:
0+1; 0+2; 0+3; 0+4;
1+1; 1+2; 1+3;
2+1; 2+2;
3+1;
5+1; 5+2; 5+3; 5+4;
6+1; 6+2; 6+3;
7+1; 7+2;
8+1;
Go to the training page to exercise this


This was for earth beads only. But this works the same for heaven beads too. So to add 6 to 1, one acitvate one heaven bead and one earth bead.
The same principle holds true for:
1+5; 1+6; 1+7; 1+8;
2+5; 2+6; 2+7;
3+5; 3+6;
4+5;
Go to the training page to exercise this
Complement to 5

If we want to add more than is available on the rod, then we have to use the complement to 5.

3 + 2 — For example, say we have 3 on a rod. And we want to add 2. We can't do that in the easy way, because we can't activate 2 beads.
So instead of adding 2, we will use the complement to 5 of 2 which is 2 = 5 - 3. So we will add 5 and remove 3. That is activate the heaven bead, and deactivate the 3 heaven beads.
The same principle holds true for:
1+4;
2+3; 2+4;
3+2; 3+3; 3+4;
4+1; 4+2; 4+3; 4+4;
Go to the training page to exercise this
Complement to 10


6 + 4 — So let's say now that we have 6 on the rod. And we want to add 4. We can't activate 4 beads. We can't use the complement to 5 either. So we use the complement to 10.
We have:4 = 10 - 6. So we add 10 and remove 6. We will add 1 on the adjacent column, and remove 6 on the current rod.
The same principle holds true for:
7+3; 7+4;
8+2; 8+3; 8+4;
9+1; 9+2; 9+3; 9+4;
1+9;
2+8; 2+9;
3+7; 3+8; 3+9;
4+6; 4+7; 4+8; 4+9;
6+4;6+9;
7+8; 7+9;
8+7; 8+8; 8+9;
9+6; 9+7; 9+8; 9+9;
Go to the training page to exercise this
Both at the same time

5 + 7 — And if you want to add 7 to 5?
Let's do it. 7 = 10 - 3. So we have to add 10 and remove 3. But ... we can't remove 3 because we have a heaven bead for 5.
So let's use the complement to 5. -3 = -5 + 2. Instead, we will remove 5 and add 2.
So to sum it up:

- Remove 3. But we will break it up into:
- Add 2
- Remove 5
- Add 10 or 1 on the adjacent column
The same principle holds true for:
5+5; 6+5; 7+5; 8+5; 9+5;
5+6; 5+7; 5+8; 5+9;
6+6; 6+7; 6+8;
7+6; 7+7;
8+6;
Go to the training page to exercise this
Automatism
Now you have to forget all about this, by practicing and practicing until it becomes an automatism, so that you don't have to think about it every time.
Don't forget that you can see real examples, played for you on the tutorial page: look at the "Simple addition", "Addition", and "Complicated addition" examples.
How to subtract 2 numbers
To perform a subtraction on the soroban, you proceed very much like you do on paper: you operate on each column, and subtract digit by digit, borrowing a carry if need be.
Say we want to subtract s (the subtrahend) to m (the minuhend). First you put the number m on the soroban. We go, digit by digit, from left to right, by subtracting the digit of s to the digit of m. If the digit of s is greater than the one of m, we make a borrow on the previous column.
All the principles that we have seen so far for the addition, will be mirrored for the subtraction. Each case will be reversed so that instead of adding we will be able to subtract.
What's left on the soroban after you have removed the digit of s, is the difference m-s.
All is good
If the digit of s is lesser than the one of m, then we simply remove the beads on the rod for the digit of m.


For example, if the digit is 4, and we need to subtract 2, then ... we remove 2 beads.
The same principle holds true for:
1-1; 2-1; 3-1; 4-1;
2-2; 3-2; 4-2;
3-3; 4-3;
6-1; 7-1; 8-1; 9-1;
7-2; 8-2; 9-2;
8-3; 9-3;
4-4; 9-4;
Go to the training page to exercise this


But this is also true for digit greater than 5. For example, to subtract 6 to 9, you remove one heaven bead and one earth bead.
We can use the same principle for:
5-5;
6-6; 6-5;
7-7; 7-6; 7-5;
8-8; 8-7; 8-6; 8-5;
9-9; 9-8; 9-7; 9-6; 9-5;
Go to the training page to exercise this
Complement to 5
The digit of s might be lesser than the digit of m, but there might not be enough beads to remove on the rod.


For example, to subtract 4 to 6, we need to use the complement to 5 for 4. 4 = 5 - 1 So we will subtract 5 and add 1. Or remove the heaven bead, and activate one earth bead.
The same principle holds true for:
5-1; 5-2; 5-3; 5-4;
6-2; 6-3; 6-4;
7-3; 7-4;
8-4;
Go to the training page to exercise this
We need to make a borrow


If the digit of s is lesser than the digit of m, we make a borrow in the previous column. Or we subtract the digit of s not the digit of m but the digit of m+10.
For example, to subtract, 4 to 3, we borrow 1 on the previous, or subtract 4 to 13.
Like seen for the addition, we use complement to 10. 4 = 10 - 6 We want to subtract 4, so we will subtract 10 and add 6. This means subtract one the previous column, and add 6 on the current column.
The same principle holds true for:
1-2; 1-3; 1-4; 1-5; 1-6; 1-7; 1-8; 1-9;
2-2; 2-3; 2-4; 2-5; 2-6; 2-7; 2-8; 2-9;
3-4; 3-5; 3-6; 3-7; 3-8; 3-9;
4-5; 4-6; 4-7; 4-8; 4-9;
5-6; 5-7; 5-8; 5-9;
6-7; 6-8; 6-9;
7-8; 7-9;
8-9;
Go to the training page to exercise this
In those cases, we can distinguish the case where we can add directly the needed beads. But there is also the case when we need to use the complement to 5 to add the needed beads. Please refer to this section in "How to add numbers".
Final word
Like previously for the addition, you need to master those techniques to the point you don't think about it each time, so that it becomes an automatism. Then, you will be able to perform subtraction at the speed of light.
It is best to go to the tutorials page to see a real example, like Simple subtraction or Subtraction or Complicated subtraction.
How to multiply 2 numbers
One of the technique to multiply a number ma (the multiplicand) with another number me (the multiplier) is to use an analog to the long multiplication algorithm you already know and do on paper. It is the recommended method to use on the soroban.
One key difference is that you do partial sum along the way instead of waiting until the end to do a multiple operand addition.
You will need to know your multiplication table [Wikipedia].
As the multiplication of decimals is commutative, one prefers to choose the multiplier as the smaller of the 2 operands.
The principle is, for each digit of the multiplicand, multiply it with each digit of the multiplier (going from left to right), beginning by the rightmost digit of ma and finishing by the leftmost one.
One digit multiplier example
Let's take an example with a one digit multiplier, 57 x 6


We put 57 (the multiplicand) at the center of the soroban(left image) and place 6 (the multiplier) on the left by letting 2 empty rows between ma and me.
We multiply 7 by 6 and put 42 at the right of ma(right image).


We can now deactivate 7 on the soroban(left image), as we are finished with it.
Then, we multiply 5 by 6 and add 30 on the soroban(right image), one column to the left from the previous product. We can now again deactivate 5, and read our final product 342.
Multiple digit multiplier

It's basically the same as above but we need to repeat the process for each digit of the multiplier.
For example, let's multiply 43 with 21, 43 x 21.

So we mutiply 3 by 2 and put 6 on the soroban(left image).

We multiply 3 by 1 and add 3 on the soroban. We can deactivate 3 (right image).

We continue with the next digit of the multiplicand 4. We multiply 4 with 2 and add 8 on the soroban (left image).

And finally, we multiply 4 by 1, and add 4 on the soroban, and deactivate 4. We got the product 903 (right image).
Decimal numbers
For number with decimals, we can put the numbers on the soroban so that the marker is placed on the decimal separator.
Or you can consider the operands as integer, and report the missing decimal at the end of the operation.
For example, to multiply 45.242 with 6.78, multiply 454242 with 678 and divide the result by 100000 aka 5 decimals.
How to divide 2 numbers
To make a division on the soroban, we also use an analog of the long division algorithm you may already know. You need to know your multiplication table [Wikipedia], and also how to perform subtraction on the soroban.
We want to divide a dividend de by a divisor do, to get a quotient q and a remainder r.
Very simple division
Let's try with a very simple division, first, to get the basic idea: 7 / 3.


We put the dividend 7 on the center of the soroban. Then let 4 empty rows on the left, and put the divisor 3(left image).
How many times will 3 go into 6 ? 2, so we put 2 on the soroban at the left of the dividend by letting one emtpy column.
We know multiply 3 by 2 and subtract the result 6 from 7, which left us with 1(right image).
So the quotient is 2 with a remainder of 1.
A one digit divisor division
Let's do something a little more complicated with a division with a dividend with multiple digits but still one digit for the divisor: 945 / 5.


How many times 5 will go into 9 ? 1 so we put 1 at he left of the 945. And then subtract 5 from 9; we are left with 4 on that column(right image).
We will have to repeat the process until the remainder is less than the divisor. So, for now, the remainder is 445 and way greater than 5, so we continue.

How many times 5 will go into 4 ? None, so we add a digit of the dividend and consider how many times 5 will go into 44 ? 8 so we put 8 at the right of 1, and at the left of the remainder, and then subtract 8 * 5 = 40 from the remainder. We are left with 45(left image).

How many times 5 will go into 45 ? 9, so we put 9 on the soroban at the right of 18, and then subtract 9 * 5 = 45, and we are left with a remainder of 0(left image).
So the quotient is 189 with a 0 remainder.
A division
Let's do 782 / 23.


How many times 2 will go into 7 ? 3, so we put 3 on the soroban. And subtract 6 from 7(right image).

Then we multiply 3 by 3, and subtract the result 9 from the remainder(left image).


How many times 2 will go into 9 ? 4, so we put 4 on the soroban and subtract 8 from 9(left image).
And then multiply 4 by 3 and subtract 12; we are left with no remainder(right image).
The quotient is 34.




